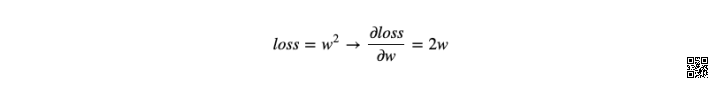π导航  

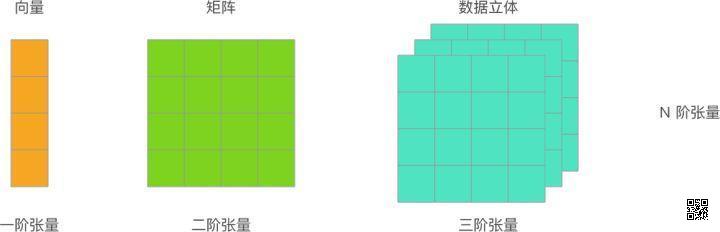
张量

首先，你应该知道什么是向量和矩阵。

我们把 1 维的数组称之为向量，

2 维的数组称之为矩阵。

那么，现在告诉你张量其实代表着更大的范围，

你也可以把其看作是N 维数组。

所以，如果现在重新描述向量和矩阵，就可以是：

一阶张量为向量，二阶张量为矩阵。

当然，零阶张量也就是标量，而更重要的是 N 阶张量，也就是 N 维数组。

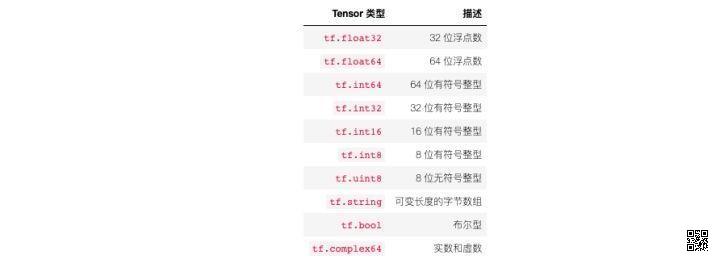
张量并不是什么晦涩难懂的概念。如果不严谨的讲，张量就是 NN 维数组。前面提到的向量、矩阵，也是张量。

后面将学习到的大多数深度学习框架都会使用张量的概念，这样做的好处是统一对数据的定义。NumPy 中，数据都使用 Ndarray 多维数组进行定义，TensorFlow 中，数据都会用张量进行表述。

下面就来学习 TensorFlow 中对张量的定义。在 TensorFlow 中，每一个 Tensor 都具备两个基础属性：数据类型（默认：float32）和形状。

其中，数据类型大致如下表所示：

根据不同的用途，TensorFlow 中主要有 2 种张量类型，分别是：

tf.Variable ：变量 Tensor，需要指定初始值，常用于定义可变参数，例如神经网络的权重。

tf.constant ：常量 Tensor，需要指定初始值，定义不变化的张量。

我们可以通过传入列表或 NumPy 数组来新建变量和常量类型的张量：

代码示例：

import tensorflow as tf

tf.__version__

输出

´2.0.0´

v = tf.Variable([[1, 2], [3, 4]]) # 形状为 (2, 2) 的二维变量

v

输出

array([[1, 2],

[3, 4]], dtype=int32)>

c = tf.constant([[1, 2], [3, 4]]) # 形状为 (2, 2) 的二维常量

c

输出

array([[1, 2],

[3, 4]], dtype=int32)>

仔细观察，你会发现输出包含了张量的 3 部分属性，分别是形状 shape，数据类型 dtype，以及对应的 NumPy 数组。

你还可以直接通过 .numpy() 输出张量的 NumPy 数组。

c.numpy()

输出

array([[1, 2],

[3, 4]], dtype=int32)

上面我们已经介绍了常量张量，这里再列举几个经常会用到的新建特殊常量张量的方法：

tf.zeros：新建指定形状且全为 0 的常量 Tensor

tf.zeros_like：参考某种形状，新建全为 0 的常量 Tensor

tf.ones：新建指定形状且全为 1 的常量 Tensor

tf.ones_like：参考某种形状，新建全为 1 的常量 Tensor

tf.fill：新建一个指定形状且全为某个标量值的常量 Tensor

c = tf.zeros([3, 3]) # 3x3 全为 0 的常量 Tensor

c

输出

array([[0., 0., 0.],

[0., 0., 0.],

[0., 0., 0.]], dtype=float32)>

tf.ones_like(c) # 与 c 形状一致全为 1 的常量 Tensor

输出

array([[1., 1., 1.],

[1., 1., 1.],

[1., 1., 1.]], dtype=float32)>

tf.fill([2, 3], 6) # 2x3 全为 6 的常量 Tensor

输出

array([[6, 6, 6],

[6, 6, 6]], dtype=int32)>

除此之外，我们还可以创建一些序列，例如：

tf.linspace：创建一个等间隔序列。

tf.range：创建一个数字序列。

tf.linspace(1.0, 10.0, 5, name="linspace")

输出

tf.range(start=1, limit=10, delta=2)

输出

实际上，如果你熟悉 NumPy 的话，你会发现这与 NumPy 中创建各式各样的多维数组方法大同小异。数据类型是一切的基础，了解完张量我们就可以继续学习张量的运算了。

Eager Execution

TensorFlow 2 带来的最大改变之一是将 1.x 的 Graph Execution（图与会话机制）更改为 Eager Execution（动态图机制）。在 1.x 版本中，低级别 TensorFlow API 首先需要定义数据流图，然后再创建 TensorFlow 会话，这一点在 2.0 中被完全舍弃。TensorFlow 2 中的 Eager Execution 是一种命令式编程环境，可立即评估操作，无需构建图。

所以说，TensorFlow 的张量运算过程可以像 NumPy 一样直观且自然了。接下来，我们以最简单的加法运算为例：

c + c # 加法计算

输出

array([[0., 0., 0.],

[0., 0., 0.],

[0., 0., 0.]], dtype=float32)>

如果你接触过 1.x 版本的 TensorFlow，你要知道一个加法运算过程十分复杂。我们需要初始化全局变量 → 建立会话 → 执行计算，最终才能打印出张量的运算结果。

init_op = tf.global_variables_initializer() # 初始化全局变量

with tf.Session() as sess: # 启动会话

sess.run(init_op)

print(sess.run(c + c)) # 执行计算

Eager Execution 带来的好处显而易见，其进一步降低了 TensorFlow 的入门门槛。之前的 Graph Execution 模式，实际上让很多人在入门时都很郁闷，因为完全不符合正常思维习惯。

TensorFlow 中提供的数学计算，包括线性代数计算方面的方法也是应有尽有，十分丰富。下面，我们再列举一个示例。

a = tf.constant([1., 2., 3., 4., 5., 6.], shape=[2, 3])

b = tf.constant([7., 8., 9., 10., 11., 12.], shape=[3, 2])

c = tf.linalg.matmul(a, b) # 矩阵乘法

c

输出

array([[ 58., 64.],

[139., 154.]], dtype=float32)>

tf.linalg.matrix_transpose(c) # 转置矩阵

输出

array([[ 58., 139.],

[ 64., 154.]], dtype=float32)>

你应该能够感觉到，这些常用 API 都能在 NumPy 中找到对应的方法，这也就是课程需要你预先熟悉 NumPy 的原因。由于函数实在太多太多。一般来讲，除了自己经常使用到的，都会在需要某种运算的时候，查阅官方文档。

所以说，你可以把 TensorFlow 理解成为 TensorFlow 式的 NumPy + 为搭建神经网络而生的 API。

自动微分

在数学中，微分是对函数的局部变化率的一种线性描述。虽然微分和导数是两个不同的概念。但是，对一元函数来说，可微与可导是完全等价的。如果你熟悉神经网络的搭建过程，应该明白梯度的重要性。而对于复杂函数的微分过程是及其麻烦的，为了提高应用效率，大部分深度学习框架都有自动微分机制。

TensorFlow 中，你可以使用 tf.GradientTape 跟踪全部运算过程，以便在必要的时候计算梯度。

w = tf.Variable([1.0]) # 新建张量

with tf.GradientTape() as tape: # 追踪梯度

loss = w * w

grad = tape.gradient(loss, w) # 计算梯度

grad

输出

上面，我们演示了一个自动微分过程，它的数学求导过程如下：

所以，当 w 等于 1 时，计算结果为 2。

tf.GradientTape 会像磁带一样记录下计算图中的梯度信息，然后使用 .gradient 即可回溯计算出任意梯度，这对于使用 TensorFlow 低阶 API 构建神经网络时更新参数非常重要。

常用模块

上面，我们已经学习了 TensorFlow 核心知识，接下来将对 TensorFlow API 中的常用模块进行简单的功能介绍。对于框架的使用，实际上就是灵活运用各种封装好的类和函数。由于 TensorFlow API 数量太多，迭代太快，所以大家要养成随时 查阅官方文档 的习惯。

tf.：包含了张量定义，变换等常用函数和类。

tf.data：输入数据处理模块，提供了像 tf.data.Dataset 等类用于封装输入数据，指定批量大小等。

tf.image：图像处理模块，提供了像图像裁剪，变换，编码，解码等类。

tf.keras：原 Keras 框架高阶 API。包含原 tf.layers 中高阶神经网络层。

tf.linalg：线性代数模块，提供了大量线性代数计算方法和类。

tf.losses：损失函数模块，用于方便神经网络定义损失函数。

tf.math：数学计算模块，提供了大量数学计算函数。

tf.saved_model：模型保存模块，可用于模型的保存和恢复。

tf.train：提供用于训练的组件，例如优化器，学习率衰减策略等。

tf.nn：提供用于构建神经网络的底层函数，以帮助实现深度神经网络各类功能层。

tf.estimator：高阶 API，提供了预创建的 Estimator 或自定义组件。

在构建深度神经网络时，TensorFlow 可以说提供了你一切想要的组件，从不同形状的张量、激活函数、神经网络层，到优化器、数据集等，一应俱全。